Quickstart

This is a minimal Tidy3D script showing the FDTD simulation of a dielectric cube in the presence of a point dipole.

Before running this notebook, make sure to have:

1. Installed tidy3d

2. Generate your free API key

3. Optional - Configured your API key

# import packages and authenticate (if needed)
import matplotlib.pylab as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web

# web.configure("YOUR API KEY GOES HERE")

First, we use the convenience class FreqRange to define the basic frequency-related parameters of the simulation.

lda0 = 0.75  # wavelength of interest (length scales are micrometers in Tidy3D)
freq0 = td.C_0 / lda0  # frequency of interest
fwidth = freq0 / 10.0  # desired freq. bandwidth

freq_range = td.FreqRange(freq0=freq0, fwidth=fwidth)  # set frequency range

Create a Structure from a Geometry like this rectangular prism Box and assign a Medium to represent its optical properties.

square = td.Structure(
    geometry=td.Box(center=(0, 0, 0), size=(1.5, 1.5, 1.5)), medium=td.Medium(permittivity=2.0)
)

Create a Source. In this case, it is a PointDipole, which is a uniform current source with a zero size.

# create source
source = td.PointDipole(
    center=(-1.5, 0, 0),  # position of the dipole
    source_time=freq_range.to_gaussian_pulse(),  # time profile of the source
    polarization="Ey",  # polarization of the dipole
)

Create a Monitor like a FieldMonitor to record electromagnetic fields in the frequency domain at freq0.

# create monitor
monitor = td.FieldMonitor(
    center=(0, 0, 0),  # center of the monitor
    size=(td.inf, td.inf, 0),  # size of the monitor
    freqs=freq_range.freqs(num_points=1),  # frequency points to record the fields at
    name="fields",
)

All these components are used to create a Tidy3D Simulation:

sim = td.Simulation(
    size=(4, 3, 3),  # simulation domain size
    grid_spec=td.GridSpec.auto(
        min_steps_per_wvl=25
    ),  # automatic nonuniform FDTD grid with 25 grids per wavelength in the material
    structures=[square],
    sources=[source],
    monitors=[monitor],
    run_time=3e-13,  # physical simulation time in second
)

# visualize in 3D
sim.plot_3d()

print(
    f"simulation grid is shaped {sim.grid.num_cells} for {int(np.prod(sim.grid.num_cells) / 1e6)} million cells."
)

simulation grid is shaped [179, 147, 147] for 3 million cells.

The python web API is used to run your simulation quickly in the cloud. The output data is stored in a SimulationData container.

# run simulation
data = td.web.run(sim, task_name="quickstart", path="data/data.hdf5", verbose=True)

11:27:54 EDT Created task 'quickstart' with task_id
             'fdve-08497039-7352-4e15-9249-73b62fad435c' and task_type 'FDTD'.

             View task using web UI at
             'https://tidy3d.simulation.cloud/workbench?taskId=fdve-08497039-735
             2-4e15-9249-73b62fad435c'.

             Task folder: 'default'.

11:28:00 EDT Maximum FlexCredit cost: 0.025. Minimum cost depends on task
             execution details. Use 'web.real_cost(task_id)' to get the billed
             FlexCredit cost after a simulation run.

             status = success

11:28:03 EDT loading simulation from data/data.hdf5

# see the log
print(data.log)

[02:49:23] INFO: Auto meshing using wavelength 0.7575 defined from sources.
           INFO: Auto meshing using wavelength 0.7575 defined from sources.
           USER: Simulation domain Nx, Ny, Nz: [179, 147, 147]
           USER: Applied symmetries: (0, 0, 0)
           USER: Number of computational grid points: 4.0184e+06.
           USER: Subpixel averaging method: SubpixelSpec(attrs={},
           dielectric=PolarizedAveraging(attrs={}, type='PolarizedAveraging'),
           metal=Staircasing(attrs={}, type='Staircasing'),
           pec=PECConformal(attrs={}, type='PECConformal',
           timestep_reduction=0.3), lossy_metal=SurfaceImpedance(attrs={},
           type='SurfaceImpedance', timestep_reduction=0.0),
           type='SubpixelSpec')
           USER: Number of time steps: 7.5090e+03
           USER: Automatic shutoff factor: 1.00e-05
           USER: Time step (s): 3.9959e-17
           USER:

           USER: Compute source modes time (s):     0.0545
[02:49:24] USER: Rest of setup time (s):            0.5844
[02:49:26] USER: Compute monitor modes time (s):    0.0001
[02:49:29] USER: Solver time (s):                   2.2550
           USER: Time-stepping speed (cells/s):     3.56e+09
           USER: Post-processing time (s):          0.2103

 ====== SOLVER LOG ======

Processing grid and structures...
Building FDTD update coefficients...
Solver setup time (s):             0.5530

Running solver for 7509 time steps...
- Time step    300 / time 1.20e-14s (  4 % done), field decay: 1.00e+00
- Time step    501 / time 2.00e-14s (  6 % done), field decay: 1.00e+00
- Time step    600 / time 2.40e-14s (  8 % done), field decay: 4.89e-01
- Time step    901 / time 3.60e-14s ( 12 % done), field decay: 3.16e-03
- Time step   1201 / time 4.80e-14s ( 16 % done), field decay: 7.81e-05
- Time step   1501 / time 6.00e-14s ( 20 % done), field decay: 2.71e-06
Field decay smaller than shutoff factor, exiting solver.
Time-stepping time (s):            1.6936
Data write time (s):               0.0081

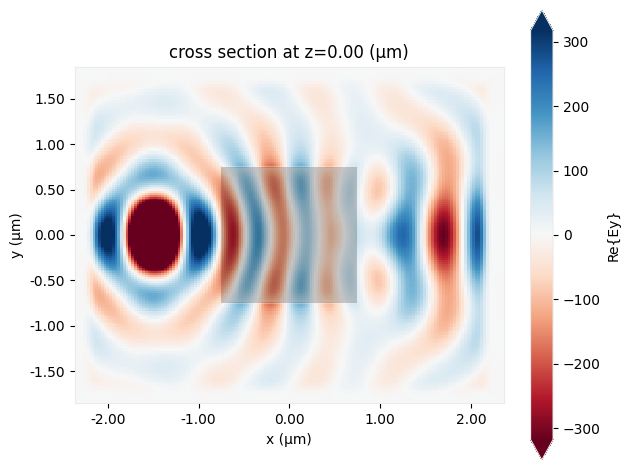
This monitor data can be easily plotted through available plot methods. You can also save, modify, and custom plot the raw FieldData and more.

# plot the field data stored in the monitor
ax = data.plot_field("fields", "Ey", z=0)

See all our examples to help you with your own designs!