8.3. Postprocessing

8.3.1. Nondimensional Outputs

The following list shows some commonly used nondimensional variables in the output files:

Table 8.3.1 Reference values for nondimensional outputs in Flow360

Property	Ref. value for nondim.	Examples in Flow360
Length	\(L_\text{gridUnit}\)	{volumeOutput, surfaceOutput}->wallDistance
Density	\(\rho_\infty\)	{surfaceOutput, volumeOutput}->primitiveVars
Velocity	\(C_\infty\)	{surfaceOutput, volumeOutput}->primitiveVars
Pressure	\(\rho_\infty C_\infty^2\)	{surfaceOutput, volumeOutput}->primitiveVars, surfaceOutput->nodeForcesPerUnitArea
Temperature	\(T_\infty\)	volumeOutput->T
Heat Flux	\(\rho_\infty C_\infty^3\)	surfaceOutput->heatFlux
Force	\(\rho_\infty C_\infty^2 L_\text{gridUnit}^2\)	force in BET output
Moment	\(\rho_\infty C_\infty^2 L_\text{gridUnit}^3\)	moment in BET output

Besides the above nondimensional quantities, there are also many coefficients commonly used in the community of computational fluid dynamics, e.g. pressure coefficient (\(C_p\)), skin friction coefficient (\(C_f\)), lift coefficient (\(C_L\)), drag coefficient (\(C_D\)), etc. Flow360 also exports the above coefficients found in volumeOutput, surfaceOutput, sliceOutput as well as the “Forces” tab of web interface.

Caution

It should be noted that the reference velocity \(U_\text{ref}\) used to calculate the \(C_p, C_f, C_D, C_L\) can be set via freestream->Mach or freestream->MachRef by users. Its definition can be found in the case configuration page. It is not the same as the reference velocity (\(C_\infty\)) used for nondimensionalization in Table 8.3.1.

The force coefficients and moment coefficients exported by Flow360 are listed in Table 8.3.2. These coefficients are shown in “Forces” tab of each case in Flow360 web portal. These coefficients can also be fetched by the flow360client.case.GetCaseTotalForces(caseId) python API call.

Table 8.3.2 Force coefficients and moment coefficients exported by Flow360

Property	Definition
CL	\(\text{Lift}/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref}\)
CD	\(\text{Drag}/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref}\)
CFx	\(\text{Force}_x/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref}\)
CFy	\(\text{Force}_y/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref}\)
CFz	\(\text{Force}_z/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref}\)
CMx	\(\text{Moment}_x/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref} L_\text{ref}\left[0\right]\)
CMy	\(\text{Moment}_y/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref} L_\text{ref}\left[1\right]\)
CMz	\(\text{Moment}_z/\frac{1}{2}\rho_\infty U_\text{ref}^2 A_\text{ref} L_\text{ref}\left[2\right]\)

Note

In the above table, all quantities in “Definition” column are dimensional.

• \(U_\text{ref} = \text{"freestream->MachRef"}\times C_\infty\).

• \(A_\text{ref} = \text{"geometry->refArea"}\times L_\text{gridUnit}^2\).

• \(L_\text{ref} = \text{"geometry->momentLength"}\times L_\text{gridUnit}\) and is an array.

The entries \(\text{"freestream->MachRef"}\), \(\text{"geometry->refArea"}\), \(\text{"geometry->momentLength"}\) correspond to the values used in the Flow360.json file.

8.3.2. History Files

At the completion of a case the Flow360 solver will generate up to 9 LOG and CSV files containing run information and the history of important variables. These LOG and CSV files can be downloaded from the WebUI or via the following python API calls:

To download the LOG files, where caseId is the alphanumeric case identifier:

flow360client.case.DownloadSolverOut('caseId', fileName='flow360_case.user.log')

To download the history CSV files please use this python API command.

Note

If your case does not contain a BET or AD model, then “bet_forces.csv” and “actuatorDisk_output.csv” will not be available.

Except for the data contained within “bet_forces.csv” and “actuatorDisk_output.csv”, all the downloadable data mentioned above can be visualized on the WebUI under the Convergence, MinMax and Forces tabs as outlined below.

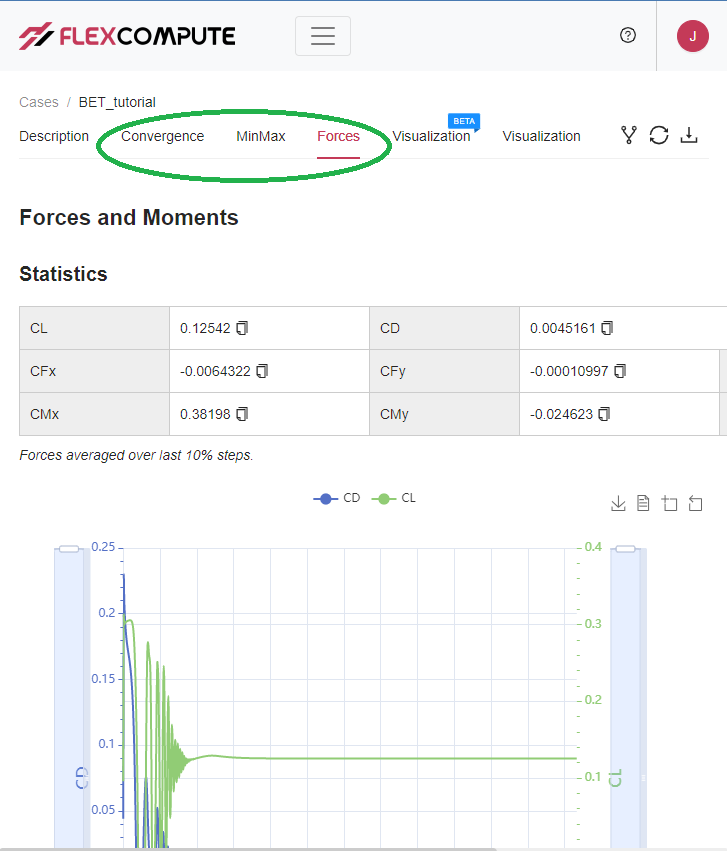
Fig. 8.3.1 Tabs to visualize key case history variables.

8.3.2.1. Actuator Disk Output

The Actuator Disk (AD) output file, “actuatorDisk_output.csv”, has the following headers: physical_step, pseudo_step, Disk0_Power, Disk0_Force, Disk0_Moment, Disk1_Power, Disk1_Force, Disk1_Moment ....DiskN_Power, DiskN_Force, DiskN_Moment for the N disks.

The power columns contains the Cp power coefficient:

(8.3.1)\[C_p = \frac{\text{Power (Watts) (kg$\cdot$m$^2$/s$^3$)}} {\rho_{\infty} C_{\infty}^3 L_\text{gridUnit}^2}\]

The Force and Moment columns simply report the constant integrated total force and moment as entered by the user.

8.3.2.2. BET Loading Output

The Blade Element Theory (BET) output file, “bet_forces.csv”, contains the time history of the following quantities:

1. Integrated x-, y-, z-component of nondimensional forces and nondimensional moments acted on each disk, represented by “Disk[diskID]_Force_x,_y,_z” and “Disk[diskID]_Moment_x,_y,_z”, respectively. The nondimensional force is defined as,

   (8.3.2)\[\text{Force}_\text{nondimensional} = \frac{\text{Force}_\text{physical} \ \text{(N)}}{\rho_\infty C_\infty^2 L_\text{gridUnit}^2}\]

   and nondimensional moment as,

   (8.3.3)\[\text{Moment}_\text{nondimensional} = \frac{\text{Moment}_\text{physical} \ \text{(N$\cdot$m)}}{\rho_\infty C_\infty^2 L_\text{gridUnit}^3}\]

   where the moment center is the centerOfRotation of each disk, defined in BETDisks of Flow360.json.

   Note

   The above Force and Moment values are forces and moments acting on the solid. Forces and moments acting on the fluid are the inverse of the above.

   Attention

   The x-, y-, z-component of Disk[diskID]_Force and Disk[diskID]_Moment is reported in the global inertial reference frame. This reference frame is defined in the mesh file.

2. Sectional thrust coefficient \(C_t\) and sectional torque coefficient \(C_q\) on each blade at several radial locations, represented by “Disk[diskID]_Blade[bladeID]_R[radialID]” with suffix “_Radius” (nondimensional), “_ThrustCoeff” and “_TorqueCoeff”. The number of radial locations is specified in nLoadingNodes.

   Note

   \(C_t\) and \(C_q\) are sectional loadings, whereas \(C_T\) and \(C_Q\) are integrated loads of the entire rotor. That is, \(C_t\bigl(r\bigr)=\frac{\text{d}C_T}{\text{d}(r/R)}\) and \(C_q\bigl(r\bigr)=\frac{\text{d}C_Q}{\text{d}(r/R)}\).

   The definition of \(C_t\) is,

   (8.3.4)\[C_t\bigl(r\bigr)=\frac{\text{Thrust per unit blade span (N/m)}}{\frac{1}{2}\rho_{\infty}\left((\Omega r)^2\right)\text{chord}_{\text{ref}}}\cdot\frac{r}{R}\]

   and \(C_q\) is,

   (8.3.5)\[C_q\bigl(r\bigr)=\frac{\text{Torque per unit blade span (N)}}{\frac{1}{2}\rho_{\infty}\left((\Omega r)^2\right)\text{chord}_{\text{ref}} \cdot R}\cdot\frac{r}{R}\]

   where \(r\) is the dimensional distance between the radial station and the axis of rotation. \(\text{chord}_\text{ref}\) is the dimensional reference chord length. \(R\) is the dimensional radius of the rotor disk.

   Important

   All the quantities in the right hand side of Eq.(8.3.2), Eq.(8.3.3), Eq.(8.3.4) and Eq.(8.3.5) are dimensional, which are different from the nondimensional values in BETDisks (list) of Flow360.json. For example, at the first disk’s first blade’s first radial location \(r=\text{Disk0_Blade0_R0_Radius}\times L_\text{gridUnit}\). The conventions for nondimensional outputs can be found at Nondimensional Outputs.

   Warning

   For steady-state simulations with BET models, the resulting \(C_t\) and \(C_q\) are only saved on the first blade, named by “Blade0”. They are written as all zeros for other blades, because all the blades have the same sectional loadings in steady BET Disk simulations. For unsteady BET Line simulations, each blade has its own \(C_t\) and \(C_q\) values.

Here is an example of the header of a “bet_forces.csv” file from a simulation containing two BET disks (assume nLoadingNodes = 20, numberOfBlades = 3 for each disk):

physical_step, pseudo_step,
Disk0_Force_x, Disk0_Force_y, Disk0_Force_z, Disk0_Moment_x, Disk0_Moment_y, Disk0_Moment_z,
Disk0_Blade0_R0_Radius, Disk0_Blade0_R0_ThrustCoeff, Disk0_Blade0_R0_TorqueCoeff,
Disk0_Blade0_R1_Radius, Disk0_Blade0_R1_ThrustCoeff, Disk0_Blade0_R1_TorqueCoeff,
...
Disk0_Blade0_R19_Radius, Disk0_Blade0_R19_ThrustCoeff, Disk0_Blade0_R19_TorqueCoeff,
Disk0_Blade1_R0_Radius, Disk0_Blade1_R0_ThrustCoeff, Disk0_Blade1_R0_TorqueCoeff,
Disk0_Blade1_R1_Radius, Disk0_Blade1_R1_ThrustCoeff, Disk0_Blade1_R1_TorqueCoeff,
...
Disk0_Blade1_R19_Radius, Disk0_Blade1_R19_ThrustCoeff, Disk0_Blade1_R19_TorqueCoeff,
Disk0_Blade2_R0_Radius, Disk0_Blade2_R0_ThrustCoeff, Disk0_Blade2_R0_TorqueCoeff,
Disk0_Blade2_R1_Radius, Disk0_Blade2_R1_ThrustCoeff, Disk0_Blade2_R1_TorqueCoeff,
...
Disk0_Blade2_R19_Radius, Disk0_Blade2_R19_ThrustCoeff, Disk0_Blade2_R19_TorqueCoeff,
Disk1_Force_x, Disk1_Force_y, Disk1_Force_z, Disk1_Moment_x, Disk1_Moment_y, Disk1_Moment_z,
...
...
...
Disk1_Blade2_R19_Radius, Disk1_Blade2_R19_ThrustCoeff, Disk1_Blade2_R19_TorqueCoeff

8.3.2.3. Aeroacoustic Output

The aeroacoustic output file has the name “total_acoustics_v3.csv” which contains the overall aeroacoustic results for all wall patches combined. If writePerSurfaceOutput has been set to true in aeroacousticOutput then “surface_NameOfPatch_acoustics_v3.csv” will also be available for each of the individual wall patches.

Each CSV file contains the following headers: “time, physical_step, observer_0_pressure, observer_1_pressure, … , observer_N_pressure, observer_0_thickness, … , observer_N_thickness, observer_0_loading, … , observer_N_loading”, where N+1 is the total number of observers specified in the aeroacousticOutput section of the case JSON file. The "_pressure" columns provide the acoustic pressure signal at the observer locations and the "_thickness" and "_loading" columns correspond to the thickness and loading noise contributions to the acoustic pressure signal.

The output file contains the non-dimensional acoustic pressure signal as a function of time, where time is the non-dimensional time specified in the first column. The second column is the physical step of the simulation at which the time is observed, assuming constant time step size.

Note

The time of observation is not necessarily contained in the simulation time as it will take a finite amount of time for the acoustic signal to propagate from the solid surfaces to the observers’ locations. As each observer can have a different distance from the solid surface, certain observers will have a proper acoustic signal before other observers at any given time. Consequently, the acoustic signal at each observer is padded with zeros at the beginning and the end of the time history, depending on the validity of the acoustic signal.

8.3.2.4. Heat Transfer

The file “surface_heat_transfer_v2.csv” contains surface integrals of the heat flux computed from nondimensional quantities. To find the dimensional heat transfer rate, multiply the nondimensional value by \(\rho_{\infty}C_{\infty}^3 L_\text{gridUnit}^2\).

8.3.3. Visualization Files

Supported visualization output formats are:

• ParaView (.pvtu)

• Tecplot (.szplt)

The export file type as well as the variables exported are selected in the Flow360.json case input file as per these conventions.

Data exports are nondimensional. Example dimensional conversions are shown below:

8.3.3.1. Velocity

Because the reference value of velocity is \(C_\infty\) from Table 8.3.1, the dimensional velocity in x-direction can be obtained by multiplying the velocityX with the freestream speed of sound. Assuming the freestream speed of sound is 340 m/s and velocityX is 0.6 in the ParaView/Tecplot file, then the dimensional velocity in x-direction is \(340 \text{ m/s} \times 0.6 = 204 \text{ m/s}\).

8.3.3.2. Pressure

The reference value of pressure is \(\rho_\infty C_\infty^2\) from Table 8.3.1. Assuming the freestream speed of sound is 340 m/s, freestream density is 1.225 kg/m ³ and p is 0.65 in the ParaView/Tecplot file, then the dimensional pressure is \(0.65 \times 1.225 \, \text{kg}/\text{m}^3 \times 340^2 \, \text{m}^2/\text{s}^2 = 92046.5 \, \text{Pa}\).

8.3.3.3. Node Force Per Unit Area

nodeForcesPerUnitArea is the total (pressure + friction) force applied at a node divided by the surface area attributed to the given node. It is particularly useful to calculate sectional loading values. If integrated over the whole surface, nodeForcesPerUnitArea would equal the total forces acting on the surface. The reference value to dimensionalize nodeForcesPerUnitArea is the same as for pressure \(\rho_\infty C_\infty^2\).

8.3.3.4. Skin Friction Coefficient

As defined, CfVec is the skin friction coefficient vector and Cf is the magnitude of that vector. To calculate the viscous stress on the wall:

(8.3.6)\[\tau_\text{wall} \ \text{(N/m$^2$)} = \text{Cf} \cdot \frac{1}{2}\rho_\infty U_{ref}^2\]

The CfVec vector is very useful to locate regions of boundary layer separation. Fully attached flow follows the surface along the streamwise direction, whereas separated flow induces local recirculation.

A strategy to investigate separation is to visualize skin friction in the streamwise direction. For example, consider flow in the x-direction over a wing, regions of negative CfVecX indicate boundary layer separation. If we set a visualization scale with 3 levels, say -1e-6, 0 and 1e-6 we will have all the negative values be one color and all the positive values be another, hence we can easily find the regions of separated flows on the surface. See the image below:

Fig. 8.3.2 The x-component of skin friction coefficient showing the attached (yellow) and separated (dark purple) flow regions on this wing at a high angle of attack.

The separated flow regions on the surface can also be visualized by using surface streamlines. Because the velocities on the surface are, by definition of a NoSlipWall, equal to 0, the key is to change the surface streamline integration parameters from velocity{X,Y,Z} to CfVec{X,Y,Z}.

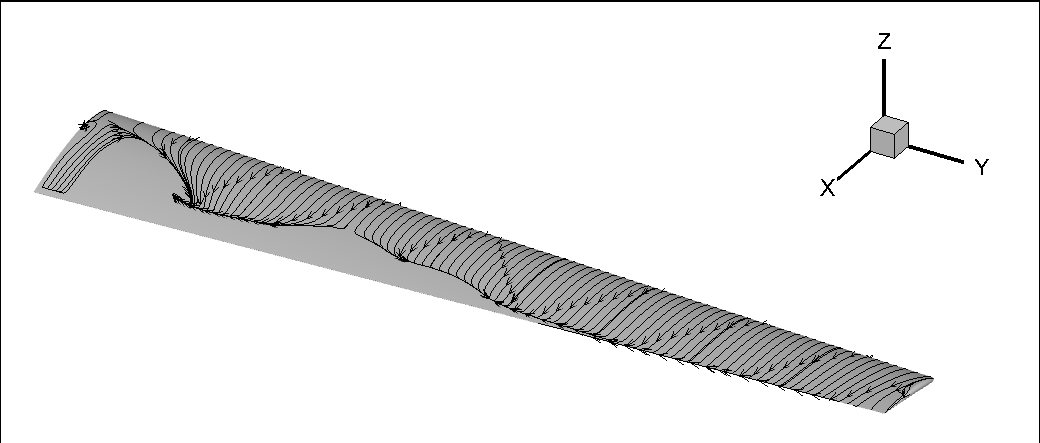
Fig. 8.3.3 Surface streamlines showing recirculation regions.

8.3.3.5. Pressure Coefficient

To calculate the dimensional pressure simply use:

(8.3.7)\[ p \ \text{(N/m$^2$)} = \text{Cp} \cdot \frac{1}{2}\rho_\infty U_\text{ref}^2 + p_\infty\]

where \(p_\infty \ \text{(N/m$^2$)}\) is the ambient pressure around the vehicle. As in the pressure at the farfield.

8.3.3.6. Total Pressure Coefficient

By definition total pressure is the sum of static pressure $p$, dynamic pressure $q$, and gravitational head. In most applications we can ignore the gravitational head. Total pressure can also be called stagnation pressure because at a stagnation point the velocity is 0, thus the dynamic pressure $q$ term becomes 0 and the total pressure becomes equal to the static pressure $p$ at that stagnation point.

As shown in equations 26 and 29 in the appendix of this paper, the total pressure coefficient \(C_{pt}\) can be calculated using the following formula:

(8.3.8)\[C_{pt} =\frac{\gamma\cdot p \cdot(1+\frac{\gamma-1}{2} \cdot \text{Mach}^2)^{\frac{\gamma}{\gamma-1}}-(1+\frac{\gamma-1}{2} \cdot \text{Mach}_\infty^2)^{\frac{\gamma}{\gamma-1}}}{(\frac{\gamma}{2} \cdot \text{Mach}_\infty^2)}\]

where the heat capacity ratio \(\gamma= 1.4\) for standard air conditions. The dimensional total pressure can be similarly calculated as with static pressure,

(8.3.9)\[ p_t \ \text{(N/m$^2$)} = C_{pt} \cdot \frac{1}{2}\rho_\infty U_\text{ref}^2 + p_t\infty\]

Just like we used CfVecX to visualize the surface separation regions above, we can use \(C_{pt}\) to visualize regions of separation in the flow volume.

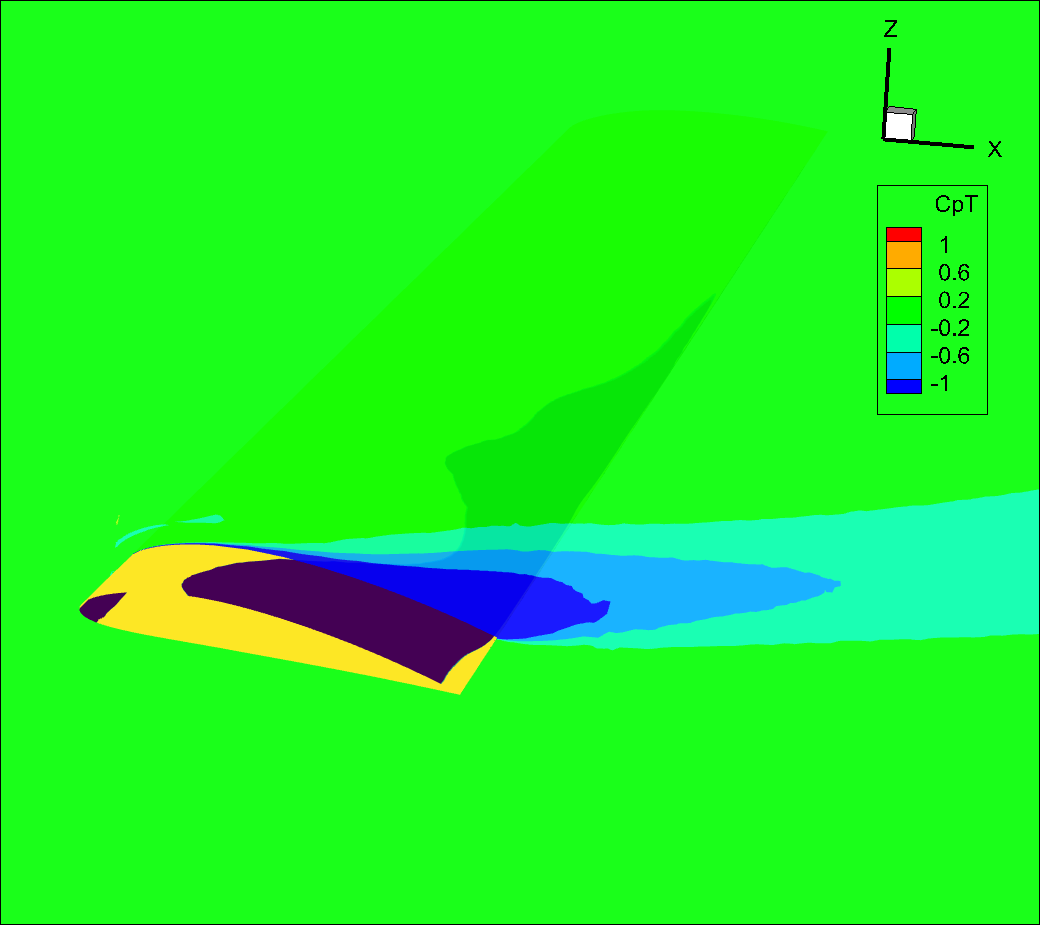
Fig. 8.3.4 Slice of total pressure coefficient showing separation region on a partially stalled wing.

The \(C_{pt}\) variable is also effective to visualize the boundary layer, if we look at the same slice as above but zoom in on the leading edge, we can see the boundary layer developing.

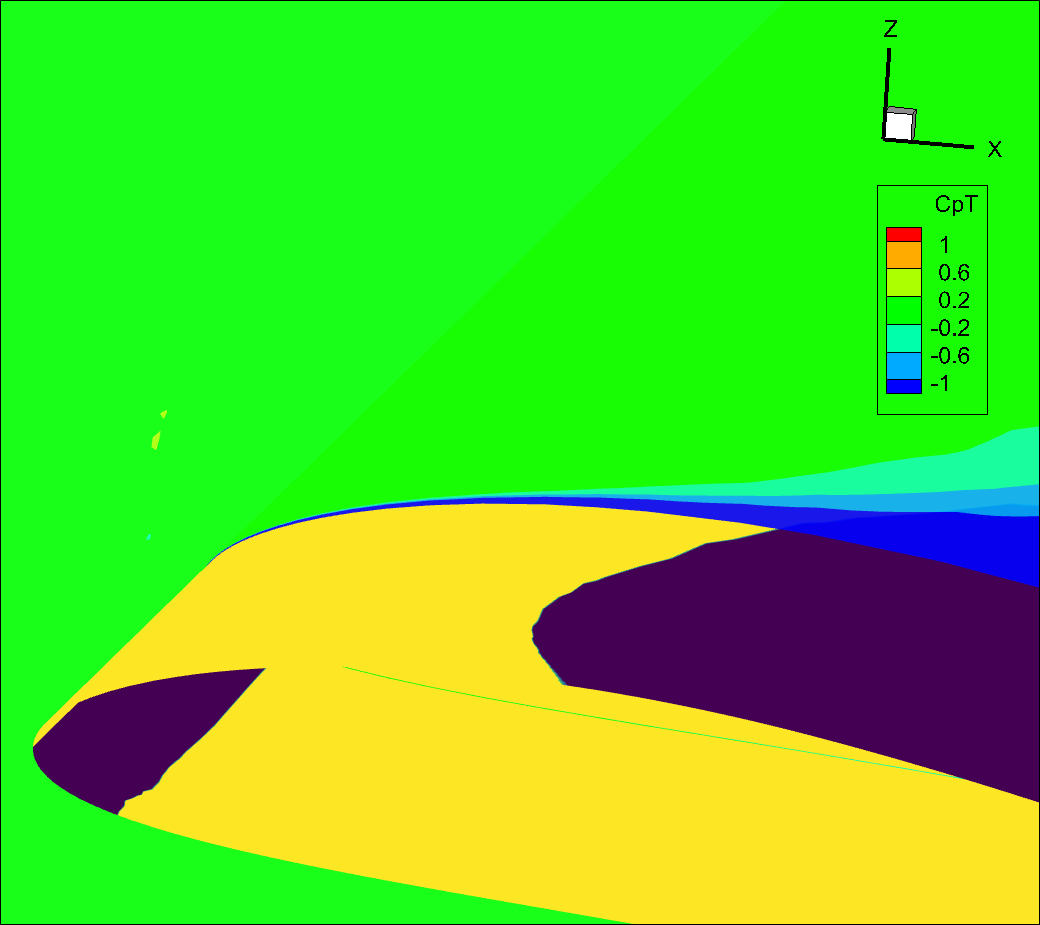
Fig. 8.3.5 Slice of total pressure coefficient showing the growing boundary layer in blue.

8.3.3.7. Q-Criterion

The qcriterion is a very convenient way to visualize vortices in your flowfield. By setting qcriterion isosurfaces in your volume solution you can easily identify vortices and gain a better understanding of their behavior. In general, for airplane type simulations, we recommend setting an isosurface value to \(\frac{\text{Mach}^2}{\text{Wing Span}^2}\). For rotor dominated flows, we typically recommend \(\frac{\text{Tip Mach}^2}{\text{Rotor Diameter}^2}\). Depending on the amount of vorticity in your flow you will have to adapt that metric value to best visualize your vortices. A larger isosurface value will only show stronger vortices. Reducing the isosurface value will visualize weaker vortices, showing more flow features but at the risk of cluttering the visualization.

Fig. 8.3.6 qcriterion isosurface showing strong tip vortex and vortices escaping from the separation region.

You will notice that, for this test case, because the volume mesh is quite coarse the qcriterion isosurface has a very jagged appearance and the vortex structures dissipate quickly.

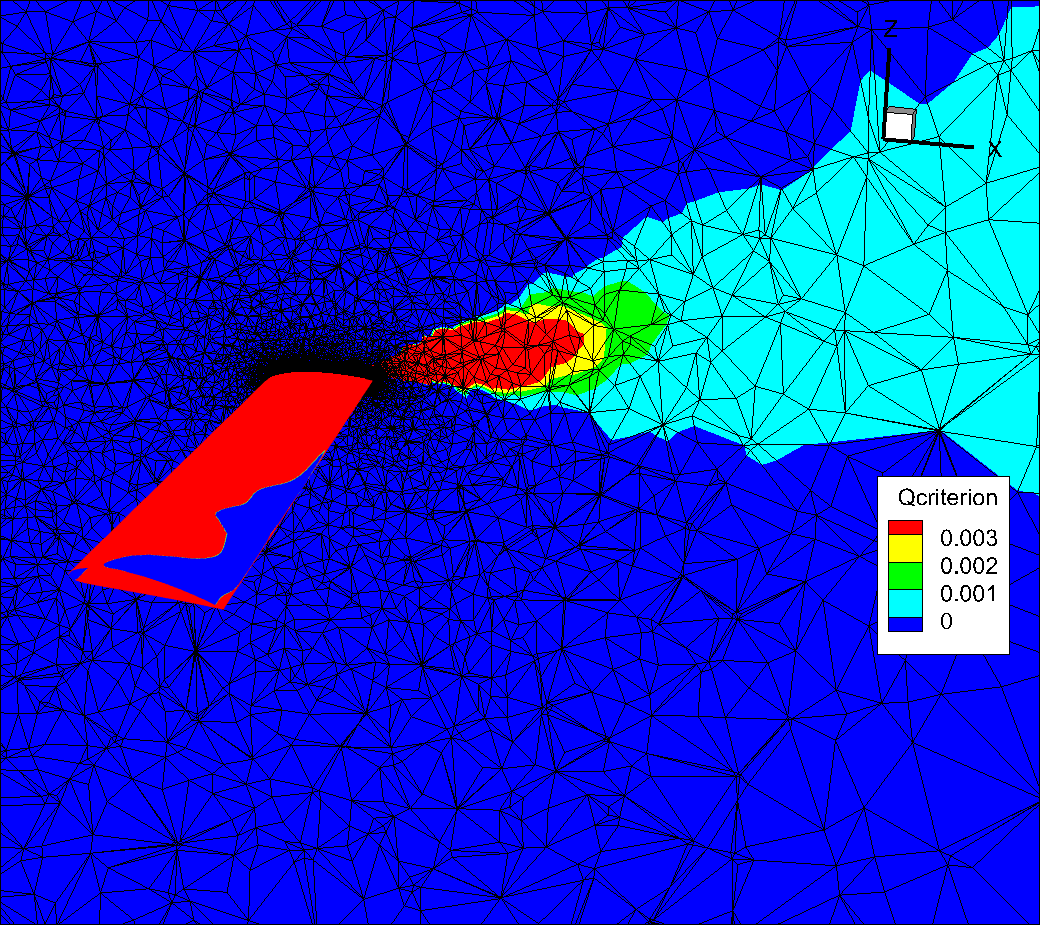
Fig. 8.3.7 Slice showing the volume mesh. Notice how quickly the mesh coarsens as we move away from the wing and how that affects the qcriterion values.

If we refine the far field substantially by applying a refinement region we can obtain a much smoother qcriterion isosurface showing improved resolution of the vortices escaping from the tip and from the separation bubble.

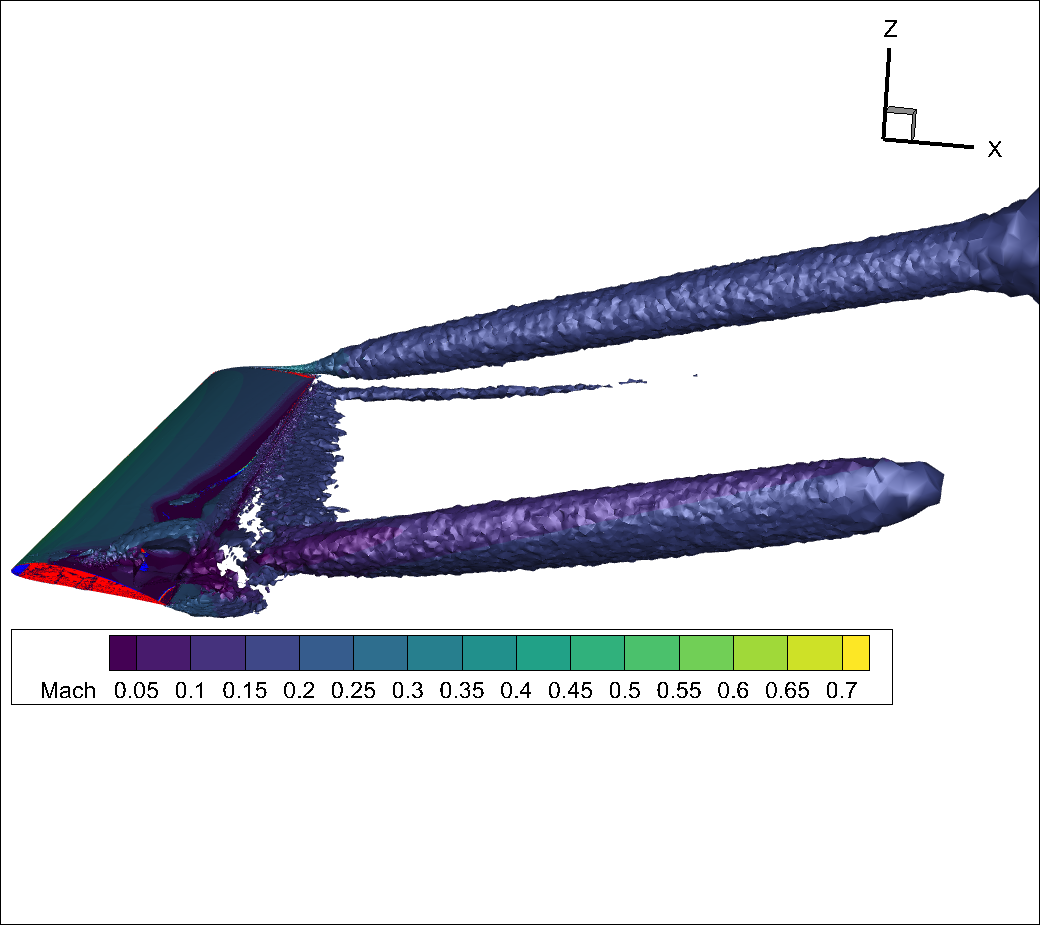
Fig. 8.3.8 qcriterion isosurface on a finer mesh showing strong tip vortex and vortices escaping from the separation region.

You will notice that now, for this refined volume mesh, the qcriterion isosurface has a much smoother appearance and the vortex structures propagate much further (i.e., are much less dissipative).

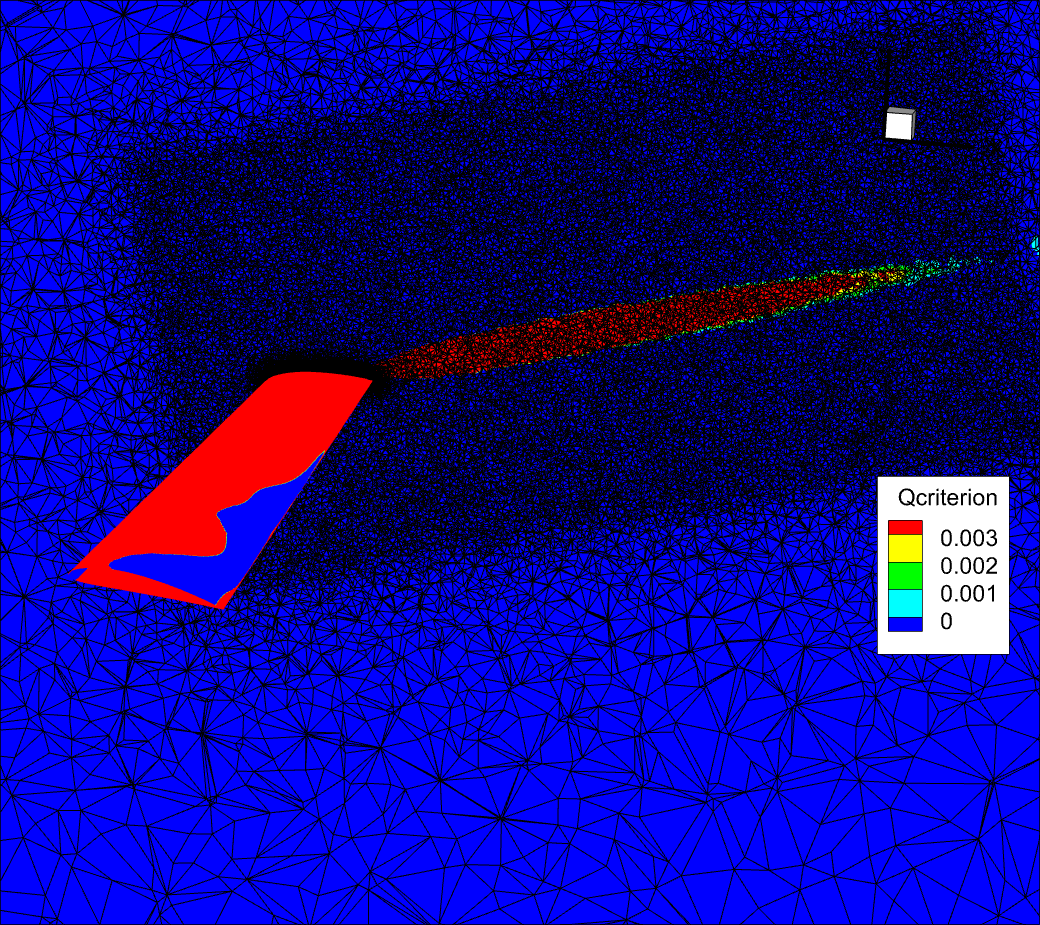
Fig. 8.3.9 Slice showing the volume mesh. Finer volume mesh showing the effect on the qcriterion dissipation.

For more flow images using the qcriterion to visualize vortices please see:

• BET Line flow visualization video

• Wind turbine case study

• Hover prediction workshop paper (figs 9 and 17)

• Rotor modeling techniques paper (figs 11, 12, 26 and 27)

• XV 15 BET simulations paper (fig 19)

• Automatic propeller modeling tool Rotor5 paper (figs 4, 18 and 19)

• XV15 DES simulations paper (figs 10, 14 and 17)

8.3.3.8. BET Visualization

An additional option betMetrics in volumeOutput is available to visualize the BET related quantities. This is demonstrated in the BET tutorial.