Tailoring directional scattering in silicon nanodisks#
The manipulation of light at the nanoscale is essential for advancing modern photonic technologies. High-index all-dielectric nanoparticles have emerged as a low-loss alternative to plasmonic structures, offering strong electric and magnetic resonances without the significant absorption losses typical of metals. A key advantage of these dielectric systems is the ability to exploit the interference between optically induced electric and magnetic modes, enabling precise control over light scattering directionality. In particular, silicon nanodisks can be engineered to achieve spectral overlap between electric and magnetic dipole resonances by adjusting their aspect ratio. This overlap leads to suppressed backscattering and enhanced forward scattering.
In this notebook, we reproduce the key results presented in Isabelle Staude, Andrey E. Miroshnichenko, Manuel Decker, Nche T. Fofang, Sheng Liu, Edward Gonzales, Jason Dominguez, Ting Shan Luk, Dragomir N. Neshev, Igal Brener, and Yuri Kivshar, "Tailoring Directional Scattering through Magnetic and Electric Resonances in Subwavelength Silicon Nanodisks", ACS NANO, (2013). DOI: https://doi.org/10.1021/nn402736f.
We begin by performing a multipole decomposition of a single silicon nanodisk to identify its electric and magnetic resonances. By varying the aspect ratio of the structure, we highlight the potential for spectral overlap between these contributions to the extinction cross-section. Next, we simulate a periodic array of nanodisks with different aspect ratios and demonstrate that backscattering is strongly suppressed when the electric and magnetic dipole resonances are spectrally aligned.

[1]:
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web
Multipole Decomposition#
First, we will sweep the disk aspect ratio and analyze the position of the electric and magnetic dipole resonance. To carry out the multipole decomposition, we will follow the methods described in this example notebook.
From the example above we will copy the function to carry out the multipole decomposition, and create a function to carry out the decomposition for a given SimulationData object.
[2]:
# function for carrying out multipole decomposition
def ME(Ex, Ey, Ez, x, y, z, eps_xx, eps_yy, eps_zz, freqs, eps_medium):
EModulus = 2 / (td.C_0 * td.EPSILON_0 * eps_medium)
# first we create the 4-dimensional (x,y,z,f) datasets
X, Y, Z, Freqs = np.meshgrid(x, y, z, freqs, indexing="ij")
# defining the angular frequencies
omega = 2 * np.pi * freqs
# import libraries to carry out integration and Bessel functions
from scipy.integrate import trapezoid as trapz
from scipy.special import spherical_jn as jn
# function for calculating the current density
J = lambda Ei, epsilon: 1j * (2 * np.pi * Freqs) * td.EPSILON_0 * (epsilon - eps_medium) * Ei
# function for calculating volume integral
integrate = lambda Data: trapz(trapz(trapz(Data, x=x, axis=0), x=y, axis=0), x=z, axis=0)
# defining the current densities
Jx = J(Ex, eps_xx)
Jy = J(Ey, eps_yy)
Jz = J(Ez, eps_zz)
# r vector
r = np.sqrt(X**2 + Y**2 + Z**2)
# wavevector
k = omega / td.C_0
# dot product k.r
kr = k * r
# dot product r.J
rj = X * Jx + Y * Jy + Z * Jz
# function for calculating dipole moments
P = lambda Ji, Xi: (1j / omega) * (
integrate(Ji * jn(0, kr))
+ ((k**2) / 2) * integrate((3 * rj * Xi - Ji * r**2) * jn(2, kr) / kr**2)
)
# dipole moments
Px = P(Jx, X)
Py = P(Jy, Y)
Pz = P(Jz, Z)
Ed = np.abs(Px) ** 2 + np.abs(Py) ** 2 + np.abs(Pz) ** 2
# cross product for calculating magnetic moments
rXJ_x = Y * Jz - Z * Jy
rXJ_y = Z * Jx - X * Jz
rXJ_z = X * Jy - Y * Jx
# dipole magnetic moments
Mx = (3 / 2) * integrate(rXJ_x * jn(1, kr) / kr)
My = (3 / 2) * integrate(rXJ_y * jn(1, kr) / kr)
Mz = (3 / 2) * integrate(rXJ_z * jn(1, kr) / kr)
Md = np.abs(Mx) ** 2 + np.abs(My) ** 2 + np.abs(Mz) ** 2
# auxiliary lists for calculating quadrupoles
coords = [X, Y, Z]
crossProd = [rXJ_x, rXJ_y, rXJ_z]
Js = [Jx, Jy, Jz]
# electric quadrupole
Eq = np.zeros(Px.shape)
for alpha in range(3):
for beta in range(3):
ra = coords[alpha]
rb = coords[beta]
ja = Js[alpha]
jb = Js[beta]
delta = 0 if alpha != beta else 1
integrand1 = (3 * (ra * jb + rb * ja) - 2 * rj * delta) * (jn(1, kr) / kr)
integrand2 = ((5 * ra * rb * rj) - (ra * jb + rb * ja) * r**2 - (r**2 * rj * delta)) * (
jn(3, kr) / kr**3
)
Eq_ab = (3j / omega) * (integrate(integrand1) + (2 * k**2) * integrate(integrand2))
Eq += (1 / 120) * np.abs(k * Eq_ab) ** 2
# magnetic quadrupole
Mq = np.zeros(Px.shape)
for alpha in range(3):
for beta in range(3):
ra = coords[alpha]
rb = coords[beta]
rxja = crossProd[alpha]
rxjb = crossProd[beta]
Mq_ab = 15 * integrate((ra * rxjb + rb * rxja) * jn(2, kr) / kr**2)
Mq += (1 / 120) * (np.abs(k * Mq_ab) ** 2) / td.C_0**2
# constants
k = (2 * np.pi * freqs) / td.C_0
const = (k**4) / (6 * np.pi * ((eps_medium * td.EPSILON_0) ** 2) * EModulus)
return Ed * const, Md * const / (td.C_0 / np.sqrt(eps_medium)) ** 2, Eq * const, Mq * const
We will also define an auxiliary function for calling the ME function for a given SimulationData object.
[3]:
def run_me(sim_data):
freqs = sim_data["fieldMon"].Ex.f.values
eps_medium = sim_data.simulation.medium.permittivity
# electric field and permittivity data
E = sim_data["fieldMon"]
Eps = sim_data["epsMon"]
eps_xx = Eps.eps_xx
eps_yy = Eps.eps_yy
eps_zz = Eps.eps_zz
Ex = E.Ex
Ey = E.Ey
Ez = E.Ez
# spatial components
x, y, z = eps_xx.x, eps_xx.y, eps_xx.z
# calling the function.
Ed, Md, Eq, Mq = ME(
Ex.values,
Ey.values,
Ez.values,
x.values,
y.values,
z.values,
eps_xx.values,
eps_yy.values,
eps_zz.values,
freqs,
eps_medium,
)
return Ed, Md, Eq, Mq
Simulation Setup#
Next we will define a function for creating the Simulation object. The model consists in a single unit cell of a Si cylinder, with the needed monitors for calculating the multipole expansion;
[4]:
# global variables
height = 0.22
index_disk = 3.5
index_medium = 1.5
disk_medium = td.Medium(permittivity=index_disk**2)
background_medium = td.Medium(permittivity=index_medium**2)
run_time = 5e-12
[5]:
def get_me_sim(radius):
# defining source and monitor frequency
wl2 = 1.7
wl1 = 0.8
freq2 = td.C_0 / wl1
freq1 = td.C_0 / wl2
freq0 = freq1 + (freq2 - freq1) / 2
fwidth = (freq2 - freq1) / 2
wl = td.C_0 / freq0
freqs = np.linspace(freq0 - fwidth, freq0 + fwidth, 101)
# defining the cylinder structure
geometry = td.Cylinder(radius=radius, length=height)
disk = td.Structure(geometry=geometry, medium=disk_medium)
# monitor and simulation size
lx = 2 * radius
ly = 2 * radius
lz = height
Lx = wl2 + lx
Ly = Lx
Lz = wl2 + lz
# adding PMLs
boundary_spec = td.BoundarySpec(x=td.Boundary.pml(), y=td.Boundary.pml(), z=td.Boundary.pml())
# TFSF source
source_TFSF = td.TFSF(
center=(geometry.center[0], geometry.center[1], -wl / 16),
size=(
lx * 1.3,
ly * 1.3,
lz + wl / 8 + 0.1,
),
source_time=td.GaussianPulse(freq0=freq0, fwidth=fwidth),
direction="+",
injection_axis=2,
)
# since the structure is smaller than the target wavelength,
# a finer mesh is required to ensure accurate results
structure_override = td.MeshOverrideStructure(
geometry=td.Box(center=source_TFSF.center, size=source_TFSF.size),
dl=(0.02,) * 3,
)
mesh_override = [structure_override]
grid_spec = td.GridSpec.auto(min_steps_per_wvl=15, override_structures=mesh_override)
# field monitor for calculating the fields
field_monitor = td.FieldMonitor(
center=geometry.center,
fields=["Ex", "Ey", "Ez"],
size=(lx * 1.2, ly * 1.2, lz * 1.2),
freqs=freqs,
name="fieldMon",
colocate=False,
)
# permittivity monitor
permittivity_monitor = td.PermittivityMonitor(
center=field_monitor.center,
size=field_monitor.size,
freqs=field_monitor.freqs,
name="epsMon",
)
sim_me = td.Simulation(
size=(Lx, Ly, Lz),
boundary_spec=boundary_spec,
grid_spec=grid_spec,
sources=[source_TFSF],
monitors=[field_monitor, permittivity_monitor],
structures=[disk],
run_time=run_time,
medium=background_medium,
)
return sim_me
Now we plot the model to make sure everything is correct.
[6]:
sim = get_me_sim(0.5)
sim.plot_3d()
plt.show()
Tuning the Electric and Magnetic Components#
Next, we perform a parameter sweep over the disk diameter to vary the aspect ratio of the structure, aiming to identify the condition where the electric and magnetic dipole resonances spectrally overlap.
[7]:
r_list = np.linspace(0.2, 0.6, 10) / 2
sims_me = {r: get_me_sim(r) for r in r_list}
batch_me = web.Batch(simulations=sims_me, folder_name="cylinders_me")
Run the batch.
[8]:
batch_data_me = batch_me.run()
20:00:33 CEST Started working on Batch containing 10 tasks.
20:00:41 CEST Maximum FlexCredit cost: 0.337 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
20:03:14 CEST Batch complete.
Carry out multipole decomposition for each simulation.
[9]:
MDs = []
EDs = []
for r in r_list:
sim_data = batch_data_me[str(r)]
Ed, Md, Eq, Mq = run_me(sim_data)
EDs.append(Ed)
MDs.append(Md)
Now, we analyze the position of the resonance peak of the electric and magnetic dipole.
[10]:
freq_ed = 1e15
freq_md = 1e15
max_ed = []
max_md = []
freqs = sim.monitors[0].freqs
for i in range(len(MDs)):
# electric and magnetic dipole contributions
Ed = np.array(EDs[i])
Md = np.array(MDs[i])
# ignore the data to the lower frequencies of the last resonance to make sure we will follow the same resonance
Ed[freqs > freq_ed] = 0
Md[freqs > freq_md] = 0
idx_ed = np.argmax(Ed)
idx_md = np.argmax(Md)
freq_ed = freqs[idx_ed]
freq_md = freqs[idx_md]
max_ed.append(td.C_0 / freqs[idx_ed])
max_md.append(td.C_0 / freqs[idx_md])
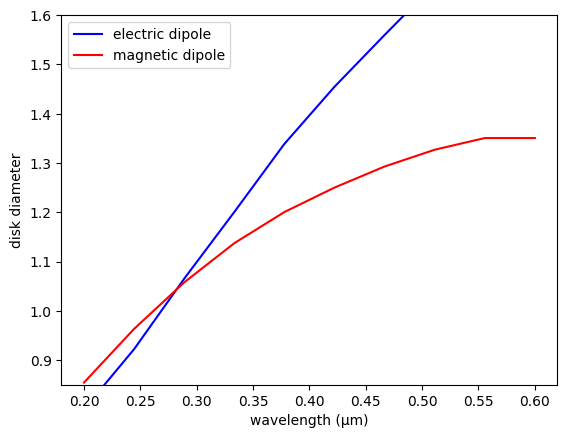
As we can see, the electric and magnetic components are at the same frequency for a disk diameter of around 0.29 µm. The results match very well the ones presented on figure 1 of the reference paper.
[11]:
fig, ax = plt.subplots()
ax.plot(2 * r_list, max_ed, label="electric dipole", color="blue")
ax.plot(2 * r_list, max_md, label="magnetic dipole", color="red")
ax.set_xlabel("wavelength (µm)")
ax.set_ylabel("disk diameter")
ax.set_ylim(0.85, 1.6)
ax.legend()
plt.show()
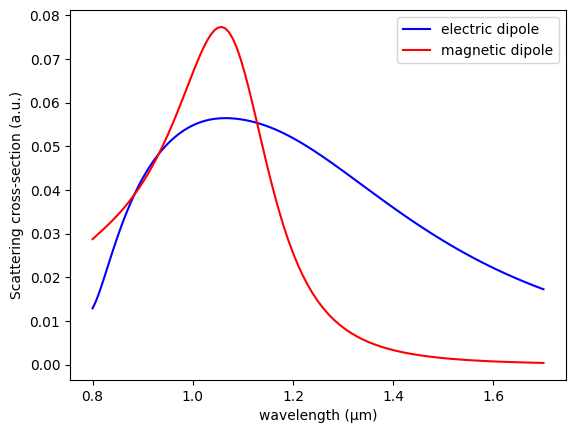
[12]:
# electric and magnetic contributions to the diameter in which the resonances are close in frequency
idx = np.argmin(abs(r_list - 0.29 / 2))
fig, ax = plt.subplots()
ax.plot(td.C_0 / freqs, EDs[idx], label="electric dipole", color="blue")
ax.plot(td.C_0 / freqs, np.array(MDs[idx]), label="magnetic dipole", color="red")
ax.set_xlabel("wavelength (µm)")
ax.set_ylabel("Scattering cross-section (a.u.)")
ax.legend()
plt.show()
Backscattering suppression#
Now, we can simulate a periodic array of disks, and analyze the spectral transmittance and reflectance. We will define another auxiliary function to return the simulation object, now with a FluxMonitor and Periodic Boundary conditions.
[13]:
def get_sim(diameter, min_steps_per_wvl=15):
# defining frequencies
wl2 = 1.65
wl1 = 1.25
freq2 = td.C_0 / wl1
freq1 = td.C_0 / wl2
freq0 = freq1 + (freq2 - freq1) / 2
fwidth = (freq2 - freq1) / 2
wl = td.C_0 / freq0
freqs = np.linspace(freq0 - fwidth, freq0 + fwidth, 101)
source_time = td.GaussianPulse(freq0=freq0, fwidth=fwidth)
radius = diameter / 2
lattice_constant = 0.8
disk = td.Structure(geometry=td.Cylinder(radius=radius, length=height), medium=disk_medium)
sim_size = (lattice_constant, lattice_constant, height + 3 * wl)
source = td.PlaneWave(
source_time=source_time,
pol_angle=0,
angle_theta=0,
center=(0, 0, -sim_size[2] / 2 + 1),
direction="+",
size=(td.inf, td.inf, 0),
)
# flux monitor
flux_mon = td.FluxMonitor(
name="flux_mon",
size=(td.inf, td.inf, 0),
center=(0, 0, sim_size[2] / 2 - 1),
freqs=freqs,
)
# field monitor
field_mon = td.FieldMonitor(name="field_mon", size=(0, 0, 0), center=(0, 0, 0), freqs=freqs)
# grid spec
grid_spec = td.GridSpec.auto(min_steps_per_wvl=min_steps_per_wvl)
boundary_spec = td.BoundarySpec(
x=td.Boundary.periodic(), y=td.Boundary.periodic(), z=td.Boundary.pml()
)
sim = td.Simulation(
size=sim_size,
center=(0, 0, 0),
grid_spec=grid_spec,
structures=[disk],
sources=[source],
monitors=[flux_mon, field_mon],
run_time=run_time,
boundary_spec=boundary_spec,
medium=background_medium,
)
return sim
Sweep over multiple disk diameters
[14]:
diameters = np.linspace(0.4, 0.6, 9)
batch = web.Batch(simulations={i: get_sim(i) for i in diameters})
batch_data = batch.run()
20:04:41 CEST Started working on Batch containing 9 tasks.
20:04:48 CEST Maximum FlexCredit cost: 0.225 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
20:30:12 CEST Batch complete.
Now we analyze the transmitted flux over all simulations, and also the points of maximum for the electric and magnetic fields.
[15]:
T = []
E_max = []
H_max = []
for d in diameters:
sim_data = batch_data[str(d)]
flux = sim_data["flux_mon"].flux
# extract E field components
Ex = sim_data["field_mon"].Ex
Ey = sim_data["field_mon"].Ey
Ez = sim_data["field_mon"].Ez
# extract H field components
Hx = sim_data["field_mon"].Hx
Hy = sim_data["field_mon"].Hy
Hz = sim_data["field_mon"].Hz
# calculate |E| and |H| (magnitude)
E = np.sqrt(np.abs(Ex) ** 2 + np.abs(Ey) ** 2 + np.abs(Ez) ** 2)
H = np.sqrt(np.abs(Hx) ** 2 + np.abs(Hy) ** 2 + np.abs(Hz) ** 2)
idx_e = E.argmax()
E_max.append(float(td.C_0 / E.f[idx_e]))
idx_m = H.argmax()
H_max.append(float(td.C_0 / H.f[idx_m]))
flux = flux.assign_coords(wl=td.C_0 / flux.coords["f"])
flux = flux.swap_dims({"f": "wl"})
flux = flux.drop_vars("f")
T.append(flux)
T = np.array(T)
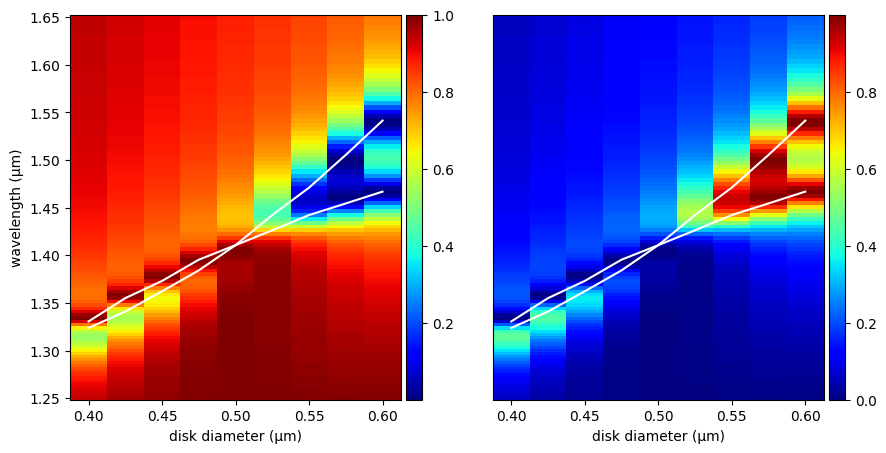
By visualizing the transmitted and reflected flux, we observe a suppression of backscattering when the magnetic and electric field resonances overlap. The results closely match figure 4 of the reference paper.
[16]:
from mpl_toolkits.axes_grid1 import make_axes_locatable
freqs = E.f
fig, ax = plt.subplots(ncols=2, figsize=(10, 5))
pm = ax[0].pcolormesh(diameters, td.C_0 / freqs, T.T, shading="auto", cmap="jet")
pm2 = ax[1].pcolormesh(diameters, td.C_0 / freqs, 1 - T.T, shading="auto", cmap="jet")
for axes, p in zip(ax, [pm, pm2]):
divider = make_axes_locatable(axes)
cax = divider.append_axes("right", size="5%", pad=0.05)
plt.colorbar(p, cax=cax)
for a in ax:
x_lim = a.get_xlim()
a.plot(diameters, E_max, color="white")
a.plot(diameters, H_max, color="white")
a.set_xlim(x_lim)
a.set_xlabel("disk diameter (µm)")
ax[0].set_ylabel("wavelength (µm)")
ax[1].tick_params(left=False, labelleft=False)
plt.show()